Nella puntata precedente si è parlato degli albori della grafica, cronologicamente parlando localizzati dai primi anni Settanta fino alla metà degli anni Ottanta. Da quel periodo e per un ulteriore decennio l’utilizzo della grafica bidimensionale fu ancora largamente diffuso, sia per ragioni tecniche (hardware commerciale non ancora performante per una grafica completamente 3D) che stilistiche: tuttavia furono sviluppate e utilizzate varie tecniche, alcune davvero fantasiose, per donare ai videogames dell’epoca un “tocco di tridimensionalità”. Prima di elencarle, però, c’è da fare un ulteriore passo indietro, necessario per marcare il momento esatto in cui iniziò concretamente lo sviluppo della computer grafica tridimensionale come così è intesa oggi.

In principio fu una teiera
Contestualmente alla ricerca pioneristica sulla realtà virtuale, culminata con l’ingegnerizzazione nel 1965 del primo head-mounted display della storia che trasmetteva immagini in 3D, iconicamente battezzato “Spada di Damocle” per via del supporto pendente dal soffitto, tra gli anni Sessanta e Settanta negli Stati Uniti fu fervente la ricerca in campo accademico per la rappresentazione computerizzata del mondo che ci circonda. I principali gruppi di ricerca in quest’ambito erano il MIT (dove fu creata appunto la “Spada di Damocle”) e l’Università dello Utah, e fu in quest’ultima che furono sviluppate le prime due effettive “trasposizioni” in grafica digitale di due oggetti reali. Nel 1972 Ivan Sutherland, dottore in fisica e oggi considerato il padre della grafica computerizzata, realizzò il primo oggetto in 3D della storia, la “scansione” in scala della carrozzeria della Volskwagen Beetle di sua moglie; tre anni dopo, Martin Newell per il suo dottorato in informatica progettò invece la riproposizione grafica di una teiera che aveva in casa.
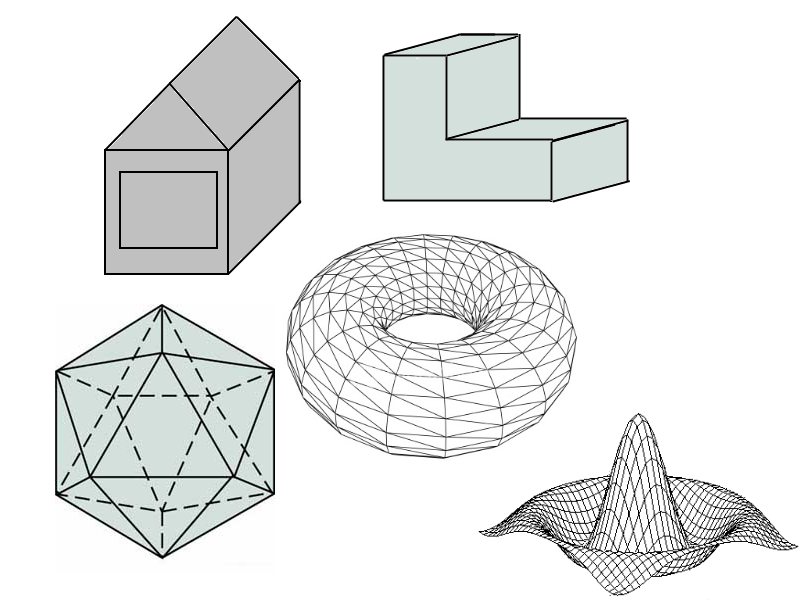
Sia Sutherland che Martin ebbero la giusta idea: affinché potessero essere riproposte graficamente, le superfici degli oggetti andavano scomposte in una mesh (maglia) poligonale, ossia in un insieme di vertici, spigoli e facce poligonali posti opportunamente in uno spazio geometrico tridimensionale. Ma mentre per il suo maggiolino Sutherland disegnò manualmente su un computer vertici e spigoli a partire da precedenti misurazioni e attraverso una tecnologia a light-pen da lui stesso sviluppata, Newell fu capace di creare la sua teiera da un modello matematico correttamente formulato e sempre riusabile, basato sulle coordinate cartesiane dei vari punti di sella sulla superficie della teiera. Perciò, sebbene la sua teiera non sia stata cronologicamente parlando il primo oggetto in grafica 3D di sempre, ha un valore storico decisamente maggiore: difatti quello oggi noto come Utah teapot o Newell teapot è il primo modello 3D della storia. Ancora oggi, nei vari software di creazione di modelli 3D, lo Utah teapot è il primo modello di riferimento, il corrispettivo per la grafica 3D dello stampare a schermo «Hello world!» per i linguaggi di programmazione, e viene sovente inserita come easter egg in videogiochi e in film in CGI.

Il mondo fatto a modelli
Come detto, l’idea di Newell di rappresentare un oggetto attraverso modelli matematici divenne la base concettuale tuttora seguita per la grafica 3D: a partire da figure solide note nella geometria euclidea o da curve definite da funzioni matematiche, era possibile comporre elementi la cui forma richiamava quella di oggetti reali, animali e qualche primitivo volto umano. In un secondo momento si passava alla visualizzazione su schermo del modello geometrico o dell’insieme di modelli (che oggi viene chiamata scena), ossia tutto il software necessario per “tradurre” in immagine 2D, attraverso calcoli matematici per la proiezione e la diffrazione della luce sull’oggetto. Questo processo viene chiamato rendering (riproposizione) e viene effettuato attraverso l’uso di algoritmi che simulano il comportamento della luce e le proprietà ottiche e fisiche degli oggetti.
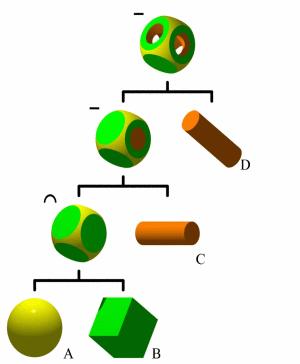
Il paradigma a due passi, realizzazione della scena di modelli prima e rendering degli stessi poi (di cui parleremo nella prossima e ultima puntata), è quello tutt’oggi utilizzato. Come detto, i modelli possono essere creati a partire da figure solide note, dette primitive, attraverso operazioni tra esse, quali rotazioni e intersezioni: ad esempio si può comporre un semplice modello di un cono gelato a partire da un cono rovesciato e da alcune sfere intersecate tra loro e con la base del cono. Questa tecnica è chiamata CSG (Constructive Solid Geometry) e può essere utilizzata sia proceduralmente, cioè attraverso algoritmi (come fece Newell con la sua teiera), sia parametricamente, cioè “componendo” manualmente la figura con editor grafici. La CSG è una tecnica molto potente, utilizzata tantissimo per la costruzione degli ambienti di gioco, sia esterni come una città o dei paesaggi rocciosi, sia interni come delle grotte o dei dungeon. I primi storici motori grafici quali il primo Unreal Engine usavano intensivamente la CSG.

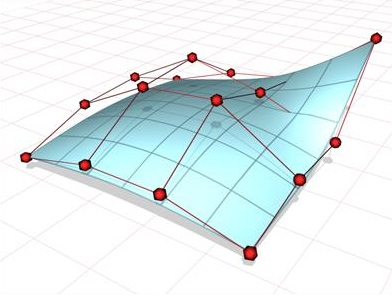
Per la composizione procedurale invece di modelli più complessi, con forme difficilmente ricavabili con la CSG, si possono usare le cosiddette funzioni spline. In passato le spline erano fascette di materiale elastico usate nel disegno tecnico per tracciare gli archi; oggi con spline si intende una funzione matematica “a pezzi”, ovvero composta da una serie di polinomi di grado definito, di solito tre, che interpolano alcuni punti definiti nello spazio detti nodi in modo tale che la funzione finale risulti continua fino ad un definito grado di derivazione. Le spline hanno largo utilizzo nell’ingegneria, ad esempio nell’automazione si utilizzano le spline per poter definire la legge matematica della traiettoria che un robot deve percorrere a partire dalle coordinate cartesiane dei punti d’interesse. Per quanto concerne la grafica viene utilizzata una particolare classe di spline dette NURBS (Non Uniform Rational Basis-Splines): le NURBS sono particolari curve la cui geometria è totalmente nota e sono molto semplici da parametrizzare, quindi si prestano particolarmente a un utilizzo su calcolatore. Nel dettaglio, oltre che dai nodi interni e dal grado dei polinomi, le NURBS vengono descritte attraverso equazioni parametriche dipendenti anche da punti esterni a essa, che ne dettano flessi e curvature, i vertici di controllo. Per il caso tridimensionale i parametri utilizzati sono le due ascisse curvilinee riferite alla superficie, di solito chiamate u e v. L’insieme di questi parametri creano un’estremamente precisa mesh poligonale composta da surface patches (pezze superficiali) e dettata dai poligoni di controllo, delimitati dai vari vertici di controllo. Inoltre le NURBS possono essere usate in composizione, attaccate ai bordi l’una dell’altra, potendo così descrivere praticamente ogni superficie immaginabile in uno spazio 3D.
Il triangolo si, è stato considerato!
La CSG è un’ottima tecnica per la rappresentazione grafica di elementi statici, ma risulta ostica da utilizzare per la rappresentazione di modelli che dovranno muoversi (l’animazione si tratterà nella prossima puntata). L’impiego di equazioni matematiche come le NURBS permettono di descrivere oggetti grafici con precisione estrema, ma esse richiedono l’utilizzo di una notevole quantità di potenza di calcolo, fino a un paio di decenni fa fuori dalla portata di un PC per l’utilizzo domestico, figurarsi per una console. La modellazione per la grafica dei videogames o di altro software che richiede continua interazione con l’utente umano, come ad esempio i simulatori, passa attraverso una tecnica più efficiente in termini di potenza di calcolo e più semplice da padroneggiare, sebbene meno precisa nel risultato finale rispetto alle spline. Si tratta della modellazione poligonale: riprendendo l’idea originale di Sutherland e del suo maggiolino, la modellazione poligonale consiste nell’approssimare la superficie dell’oggetto da riproporre utilizzando poligoni piani, in particolare triangoli, da posizionare manualmente dal modellista a partire o da precedenti modelli 3D più precisi oppure da misure relative prese sull’oggetto fisico.

Perché i triangoli? È molto semplice: dalla geometria euclidea è noto che uno dei modi per descrivere univocamente un piano è definire tre punti tra loro distinti e che non giacciono sulla stessa retta. Siccome tre punti distinti delimitano anche un triangolo, ecco il motivo per cui si usano principalmente i triangoli per definire porzioni di superficie, e le loro relative normali (che si utilizzano per il comportamento della luce, se ne parlerà nel prossimo episodio). L’elemento base del modello poligonale è il vertice (vertex), definito esattamente come nella geometria euclidea, ossia un punto nello spazio 3D su cui convergono almeno tre spigoli (edge). Tre spigoli delimitano una faccia (face) triangolare, che appunto identifica un piano nello spazio 3D. Ovviamente possono essere utilizzate anche facce con più vertici, come i quadrilateri o i pentagoni, soprattutto per coprire regioni sferiche o comunque bombate, come i volti umani ad esempio, a patto però che i loro vertici giacciano sullo stesso piano (è facile descrivere quadrilateri i cui vertici non siano complanari). Ogni faccia è anche un poligono (polygon), ma se nel modello compaiono due o più facce complanari, ad esempio su una superficie piana, allora con poligono si intende l’insieme di quelle facce. Inoltre i software di modellazione poligonale permettono di associare ad ogni faccia e/o poligono un materiale, ossia una serie di proprietà sull’opacità e sulla diffrazione della luce che simulano quelle dei reali materiali con cui gli oggetti sono fatti, necessaria per favorire il successivo rendering: ma di questo se ne parlerà nell’episodio seguente.
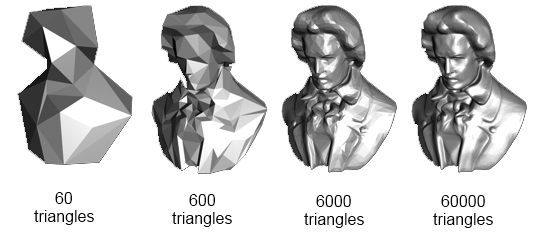
La bontà e la precisione di un modello prodotto tramite la modellazione poligonale è data dalla sua risoluzione, approssimativamente ricavabile dal numero di facce e/o poligoni utilizzati per il modello. Ovviamente, più un modello è dettagliato, più la sua grafica appare convincente, a spese però della maggiore quantità di informazioni necessaria a memorizzare il modello risultante. Già, la memoria: lo spauracchio delle scorse generazioni è anche in questo caso l’arbitro delle scelte progettuali. Però se per le console degli anni Novanta scendere a compromessi con la memoria disponibile era ancora doveroso, il mercato PC proponeva già dispositivi con decine se non centinaia di MB di RAM e schede d’accelerazione grafica con memoria dedicata, facendo finalmente decadere la “tirannia” della memoria. Comunque i primi risultati apprezzabili della grafica 3D nei videogames si ebbe su tutte le piattaforme già agli inizi degli anni Novanta, ad esempio in Alone in the dark (1992) o Star Fox (1993), nonché nei giochi da sala, come per il primo Virtual Fighter (1993).

Voxel su voxel
La modellazione poligonale si basa esclusivamente sui dettami della geometria euclidea; si può tranquillamente affermare come essa sia il corrispettivo in 3D della grafica vettoriale bidimensionale. Esiste anche una tecnica per rappresentare uno spazio tridimensionale che si basa invece sulla scomposizione in semplici unità, controparte della grafica raster 2D? La risposta è affermativa, ed è anche molto semplice: esattamente come per un’immagine bidimensionale raster, è possibile tassellare uno spazio volumetrico tridimensionale a partire da elementi infinitesimali, caratterizzati dalla loro posizione relativa ad una tripla di coordinate cartesiane e altre proprietà, come ad esempio il colore. Questo elemento è il voxel (volume element), e altro non è che il “parente” con una dimensione in più del pixel.

La tecnica per poter sviluppare modelli attraverso i voxel è detta modellazione volumetrica: il modello viene costruito impilando, manualmente oppure proceduralmente attraverso formule matematiche note, i voxel fino a quando non formano il modello desiderato, anche detto data set. In sostanza i modelli si costruiscono “montandoli” pezzo pezzo, come se fossero dei LEGO. A ogni voxel come detto si associano varie proprietà oltre alle ovvie coordinate spaziali, come il semplice colore, preso dalla palette o in codifica RGB, la densità, l’opacità, il materiale, l’indice di rifrazione della luce, che servono anch’esse per il rendering seguente del modello in un’immagine bidimensionale. I modelli finali risultanti erano già “pronti all’uso” per la fase di animazione e di rendering e non dovevano passare, come per i modelli poligonali, attraverso la fase di texturing (se ne parlerà nella puntata seguente), ma in generale erano più “pesanti” in termini di memoria e avevano un aspetto meno realistico rispetto alle controparti poligonali.
Per il rendering volumetrico è necessario definire una telecamera nello spazio relativo al volume: difatti, un data set altro non è che un campionamento dello spazio volumetrico, nel quale ogni campione (i voxel) detiene la propria quantità di trasparenza e colore, che ovviamente è variabile al variare dell’inquadratura. Definita l’inquadratura, si ricava l’immagine raster, i cui pixel sono definiti di solito tramite la codifica RGBA, dove la A finale è il valore di canale alfa, che ne regola la trasparenza.

Nei primi anni dopo lo sdoganamento della grafica 3D nei videogames, c’è stata una sorta di rivalità tra l’utilizzo della modellazione poligonale e quella volumetrica: difatti alcuni giochi con grafica 3D degli anni Novanta, tra i quali anche titoli molto famosi come Blade Runner (1997), Sid Meyer’s Alpha Centauri (1999) o Outcast (1999), utilizzavano motori grafici con modellazione dei voxel. Oggi invece tale tecnica non viene più utilizzata per lo sviluppo di videogames, completamente oscurata da quella poligonale, più versatile e che offre risultati qualitativamente migliori: tuttavia, per mera scelta stilistica, alcuni videogiochi della nostra generazione, quasi tutti di sviluppo indipendente, sono stati creati con la modellazione volumetrica, come ad esempio 7 Days to Die (2013), 3D Dot Game Heroes (2010), Space Engineers (2013) e soprattutto l’arcinoto Minecraft (2009). Oggi la modellazione e il rendering volumetrico trovano ampio utilizzo nell’ingegneria e nella medicina, principalmente per l’acquisizione e lo studio di esami strumentali quali risonanze magnetiche e scintigrafie tridimensionali.
L’illusione della profondità
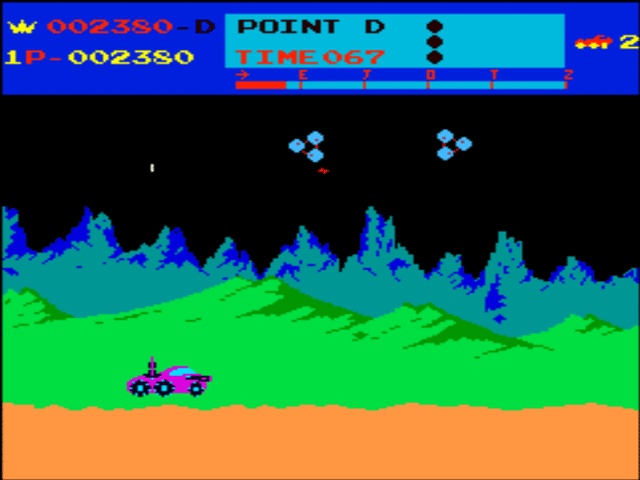
Come detto in precedenza, la grafica 3D è entrata prepotentemente nell’universo videoludico solo durante gli anni Novanta per una serie di motivazioni tecniche, quali ad esempio hardware commerciale in genere non ancora performante per l’accelerazione grafica 3D e costi di sviluppo eccessivi. Tuttavia, nel corso degli anni in cui la grafica 2D raster era ancora lo standard di fatto, gli sviluppatori hanno utilizzato vari escamotage per cercare di donare ai propri titoli una dose di “realismo tridimensionale”. Molti di essi erano basati su tecniche di prospettiva, simili a quelle usate nella pittura e nella stampa nel corso dei secoli, che davano l’illusione di un’immagine “profonda”, sebbene fosse sempre su un piano bidimensionale. Ad esempio in alcuni titoli della prima metà degli anni Ottanta, come Moon Patrol (1982) o Jungle Hunt (1982) fu implementato il cosiddetto parallax scrolling (scorrimento in parallasse): l’illusione era data pilotando il fascio elettronico del CRT in modo tale che aggiornasse più velocemente le righe in basso, dove si trovavano gli sprite del personaggio e dei nemici, e più lentamente quelle in alto, dove era localizzato lo sfondo. In questo modo si creava uno scorrimento a più velocità, simulando l’effetto profondità tipico della carrellata cinematografica.

La tecnica del parallax scrolling è stata in seguito perfezionata, lavorando non sulla velocità di scorrimento dello schermo CRT, ma sulla frequenza di refresh di sprite e dei livelli di sfondo. Regina del perfezionamento di questa tecnica nella seconda metà degli anni Ottanta fu CapCom, che con le sue schede arcade CPS crearono dei prodigi grafici per l’epoca, anche grazie all’utilizzo di sprite enormi ed estremamente dettagliati, qualcosa come 64×128 pixel complessivi per uno sprite su schermo di risoluzione 384×224 pixel con palette di colori a 16 bit e possibilità massima di 256 sprite a ogni frame (si ricorda che con sprite si intende la piastrella, non tutta la figura del personaggio!). Indimenticabili i loro beat ’em up quali Final Fight (1989), Strider (1989) e Captain Commando (1991). Anche SEGA e Nintendo utilizzarono questa tecnica per alcuni dei loro titoli celebri, come Altered Beast (1989) e Streets of Rage (1991) per la prima e Super Mario World (1990), oltre ai porting dei vari capitoli di Final Fight, per la seconda.
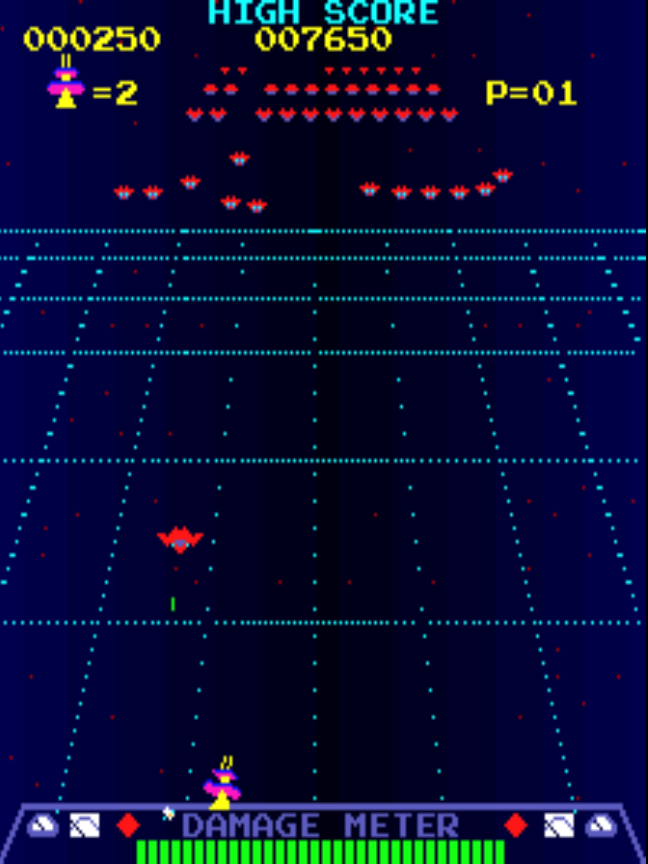
Un’altra tecnica consisteva nel “prendere in prestito” dalla grafica vettoriale l’effetto da punto di fuga prospettico: anziché fissarlo sulla posizione fisica del pennello elettrico, esso veniva definito in coordinate cartesiane, solitamente in alto al centro. L’effetto di profondità veniva conferito grazie al cosiddetto sprite scaling (scalatura degli sprite): il personaggio controllato dal giocatore era fissato in basso, mentre i nemici erano in alto e ad essi venivano associati più sprite di risoluzione diversa. Più il nemico era vicino al punto di fuga, più il suo sprite era piccolo rispetto a quello del giocatore, e viceversa. Tale tecnica si prestava molto per i videogiochi sparatutto spaziali, difatti il primo titolo che la sfruttò fu Radar Scope (1980), mentre titoli celebri che utilizzavano questa tecnica erano altri storici videogiochi SEGA come Out-Run (1986), Hang-On (1985) e Space Harrier (1986).

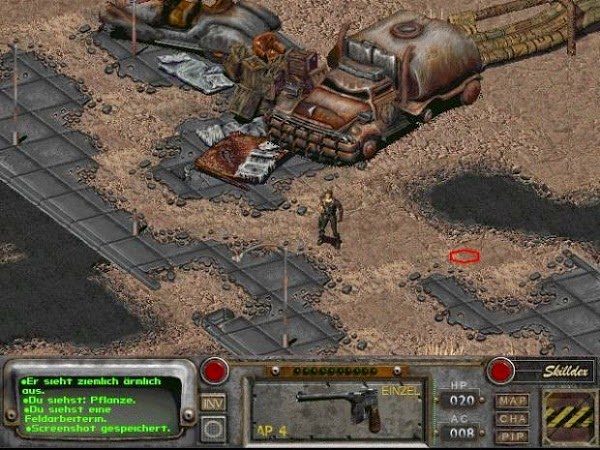
Altri videogiochi invece utilizzavano la visuale isometrica, che rappresenta una scena tridimensionale mantenendo le proporzioni degli oggetti lungo tutti i tre assi dello spazio, senza punto di fuga. In geometria l’assonometria isometrica propriamente detta si ha quando le proiezioni dei tre assi dello spazio formano angoli uniformi di 120° tra loro, in realtà la visuale in questi videogiochi è in realtà in assonometria dimetrica, ossia innalzata rispetto l’area di gioco e con un angolo di circa 45°, tuttavia si utilizza tranquillamente la nomenclatura isometrica. La proiezione è parallela, cioè non c’è prospettiva e quindi gli oggetti più distanti non diventano più piccoli. I primi videogiochi più famosi ad usare questa tecnica furono Q*Bert (1982) e Zaxxon (1982), ma divenne celebre su PC, con i giochi di ruolo come i primi capitoli delle saghe di Fallout e Diablo e con gli strategici in tempo reale o in breve RTS come le saghe di Age of Empires e Civilization.
Infine, più di una menzione d’onore va fatta a Nintendo, e in particolare al suo metodo unico e strabiliante nonostante le potenzialità tecniche limitate del suo SNES nel creare l’illusione di profondità nei suoi storici videogiochi per quella console: il mode 7. Il chip grafico dello SNES lavorava le immagini da trasmettere a schermo su otto livelli logici, chiamati modes: il primo (mode 0) era destinato di solito agli sprites dei personaggi e dei nemici, il secondo (mode 1) a quelli degli ostacoli ambientali e delle piattaforme, e così via fino all’ottavo mode, chiamato appunto mode 7. Questo mode, al costo di maggiore calcolo grafico richiesto alla macchina, permetteva al livello assegnato, solitamente lo sfondo, di poter essere ruotato e scalato a piacimento sulla base delle scanlines, riuscendo così ad ottenere effetti ottici incredibili per l’epoca.
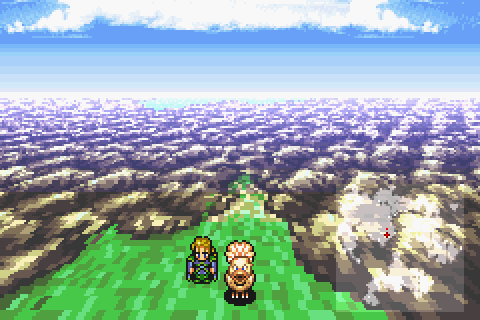
Il più famoso di essi fu senza dubbio l’effetto “orizzonte” creato attraverso una scalatura graduale degli sprite, maggiore sulla parte alta della figura e minore in basso, ed una inclinazione di circa 30° delle tile rispetto allo sprite del personaggio. Indimenticabile ad esempio il risultato finale che si osservava durante l’esplorazione, in aeronave o in sella ad un chocobo, del mondo di Final Fantasy VI (1994), oppure la visuale dei tracciati in F-Zero (1991) e Super Mario Kart (1993). Il mode 7 veniva utilizzato anche per animazioni di transizione effettuate attraverso rotazione e zoom di un frame, come ad esempio in Actraiser (1990) e in The Legend of Zelda: A link to the past (1991), oppure per le animazioni di entrata e sconfitta dei boss, ad esempio in Super Mario World 2: Yoshi’s Island (1995), con la sua indimenticata grafica a pastello. Nintendo fu anche tra le prime a utilizzare della vera grafica poligonale per gli sprite, adattata però a una grafica raster tramite un processo chiamato sprite rendering, che verrà spiegato nel prossimo episodio.

