In quanto uno degli sport più popolari sul pianeta, il calcio è sempre stato seguito da un gran numero di persone. Negli ultimi anni si sono cominciati a raccogliere nuovi tipi di informazioni sulle varie partite nelle diverse nazioni, come per esempio i dati, partita per partita, che esprimono la qualità di un tiro o di un passaggio effettuati all’interno del match. La collezione e l’elaborazione di questi dati ha posto la data science in un posto di rilievo nell’industria calcistica con diversi tipi di utilizzo e applicazioni, come l’analisi tattica delle partite, la valutazione dei giocatori da inserire in squadra, ma soprattutto la predizione del risultato. Un elemento particolarmente importante della data science nel calcio è, infatti, l’abilità di valutare la performance di una squadra in una partita, usando poi quella informazione per provare a predire il risultato delle partite successive basandosi sugli stessi dati.
Che cos’è la Data Science e il suo legame con il mondo del calcio
La scienza dei dati, in inglese data science, è l’insieme di principi metodologici e tecniche multidisciplinari volto a interpretare ed estrarre conoscenza dai dati. I metodi della scienza dei dati si basano su tecniche proveniente da varie discipline, principalmente da matematica, statistica, scienza dell’informazione, e informatica, in particolar modo dal mondo dell’intelligenza artificiale (a cui theWise Magazine ha già dedicato una serie di articoli). Per chi crede che l’adozione delle statistiche nel mondo del calcio sia una pratica recente, la storia ci fornisce un’altra versione. Negli anni Cinquanta, il ragioniere e appassionato di calcio Charles Reep iniziò ad annotare minuziosamente le statistiche delle partite di calcio cui assisteva. Reep registrava sul suo taccuino passaggi, gol, falli, tempistiche, insomma tutti i dati che gli sembravano rilevanti, alla ricerca di schemi e pattern ricorrenti, e arrivò alla conclusione – una conclusione poi sbugiardata nel corso del tempo – che la tattica migliore fosse giocare di contropiede. Nacque così la cosiddetta teoria della palla lunga, che ispirò per anni, con successi altalenanti, le strategie del calcio inglese. Andando avanti nel tempo, il primo a portare l’utilizzo del computer nel calcio è stato il Colonnello Lobanovsky (allenatore dell’Unione Sovietica e delle Dinamo Kiev), addirittura negli anni Settanta. L’analisi statistica quasi scompare dal mondo del calcio per tre decenni, almeno fino a un paio di decenni fa, quando nel panorama internazionale sono apparse aziende come Opta e Prozone (oggi Stats): i più grandi database di statistiche sportive in circolazione. Il loro modello è semplice: raccogliere quanti più dati possibili sui maggiori eventi sportivi internazionali per poi fornirli a team professionistici, agenzie di scommesse sportive e media. Si può fare l’esempio di squadre che hanno stretto legami con aziende operanti nel settore: tra queste figurano la Roma, che dal 2016 collabora con la società californiana tag.bio, e il Manchester City, che di recente ha firmato una partnership con la società SAP.
Il modello statistico probabilmente più affermato nel mondo del calcio è quello degli expected goals. Inizialmente si stima la “qualità” di un’occasione a rete, intesa come la sua percentuale di convertirsi in gol, in base a distanza e angolo di tiro insieme ad altri fattori; poi, a partire da qui, si crea un indice in grado di rappresentare il potenziale offensivo prodotto da una squadra in una determinata partita o in un numero scelto di partite. Il risultato finale è un numero che traduce i gol che ci si sarebbe aspettati (in questo senso i “goals” sono “expected”) che quella squadra o quel giocatore avessero segnato. Se tutto fosse andato bene. Se non fossero intervenuti, cioè, tutti quei fattori che rendono il calcio (come ogni altro sport, anche quelli più adatti alle analisi statistiche) in gran parte imprevedibile.
Facciamo un esempio
Segue qui una traduzione, rielaborata, di un articolo scritto da David Shean sul proprio blog, in cui si propone un modello statistico scritto nel linguaggio di programmazione Python. Come si potrà notare, si è partiti da delle ipotesi che semplificano il gioco delle squadre, necessarie a sviluppare il modello: pertanto i risultati saranno pregiudicati dalle semplificazioni adoperate. Il modello si basa sul numero di gol segnati e concessi da ogni squadra: le squadra che hanno segnato di più nel passato avranno una probabilità maggiore di segnare gol nel futuro. Importiamo i risultati di tutte le partite recentemente conclusesi nella stagione 2016/17 di Premier League. È possibile utilizzare diverse fonti per ricavare questi dati, come ad esempio football-data.co.uk.
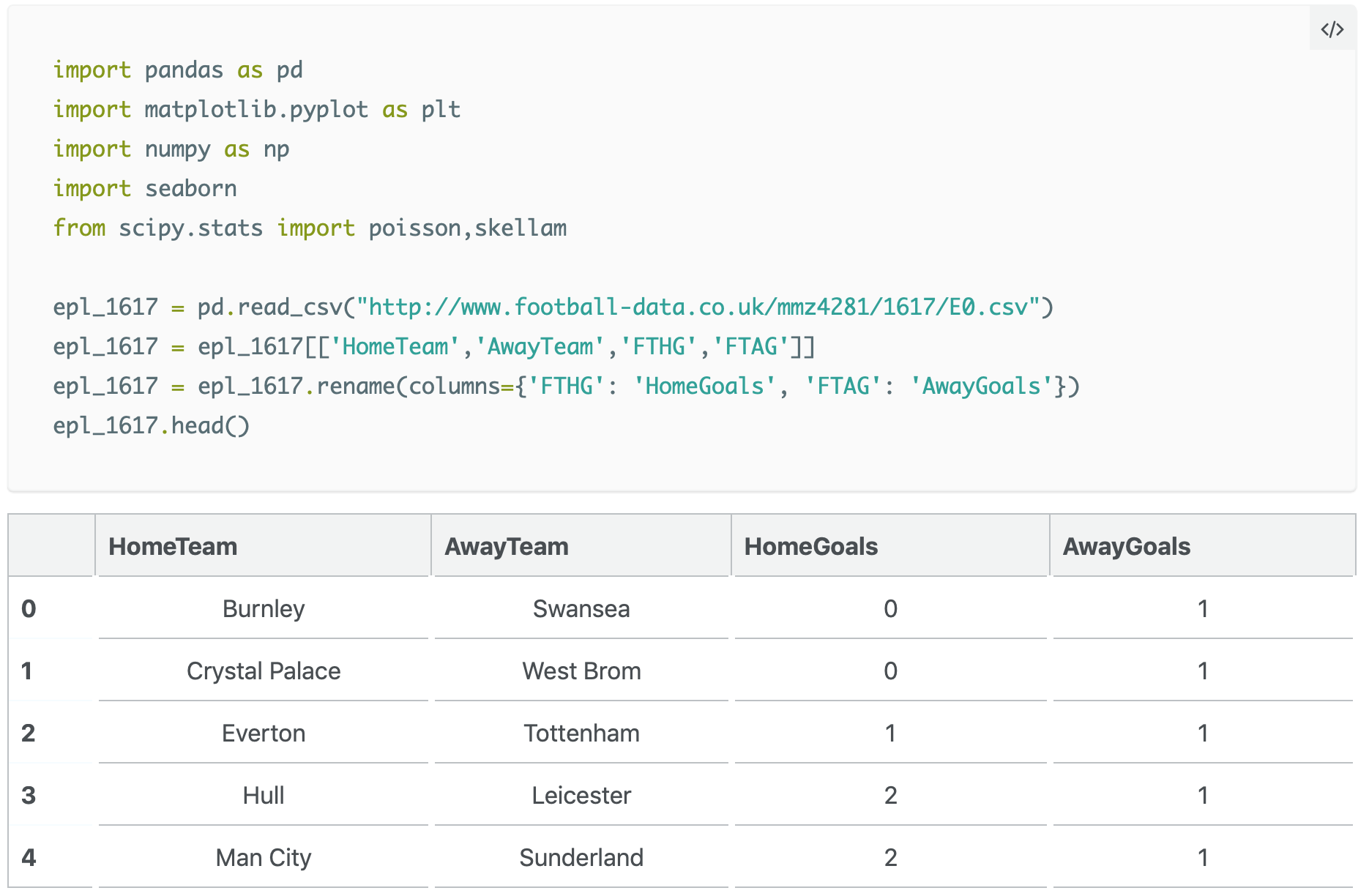
I dati, in formato file csv, sono importati in Python attraverso la libreria pandas come un dataframe, che contiene diverse informazioni per ognuna delle 380 partite disputatesi in stagione; di queste informazioni selezioniamo ciò a cui siamo interessati, ossia il nome delle squadre e il numero di gol segnati da ciascuna. Scartiamo inoltre le partite dell’ultima giornata di campionato, in quanto sono quelle su cui andremo a testare il modello.
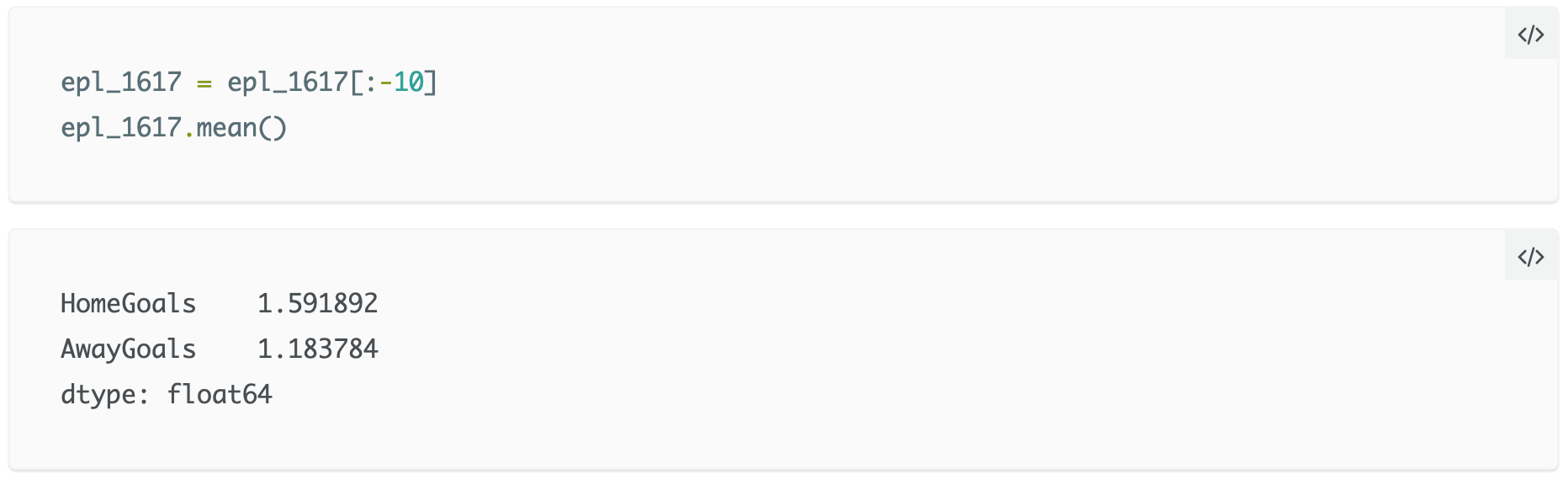
Si può notare che, mediamente, la squadra di casa segna più gol di quella in trasferta: è il cosiddetto “vantaggio casalingo”. A questo punto è tempo di introdurre la distribuzione di Poisson: è una distribuzione di probabilità discreta che descrive la probabilità che un determinato evento avvenga un certo numero di volte in un preciso periodo di tempo (per esempio, novanta minuti in una partita di calcio), con un tasso medio noto di occorrenza. Un’ipotesi chiave qui è che il numero di eventi sia indipendente dal tempo: nel nostro contesto, significa che segnare un gol non diventi più facile o più difficile in base al momento della partita o al risultato pre-esistente. Il numero di gol è invece espresso come funzione del tasso medio di gol: se non è chiaro, forse la formulazione matematica di quanto detto può aiutare a schiarirsi le idee:
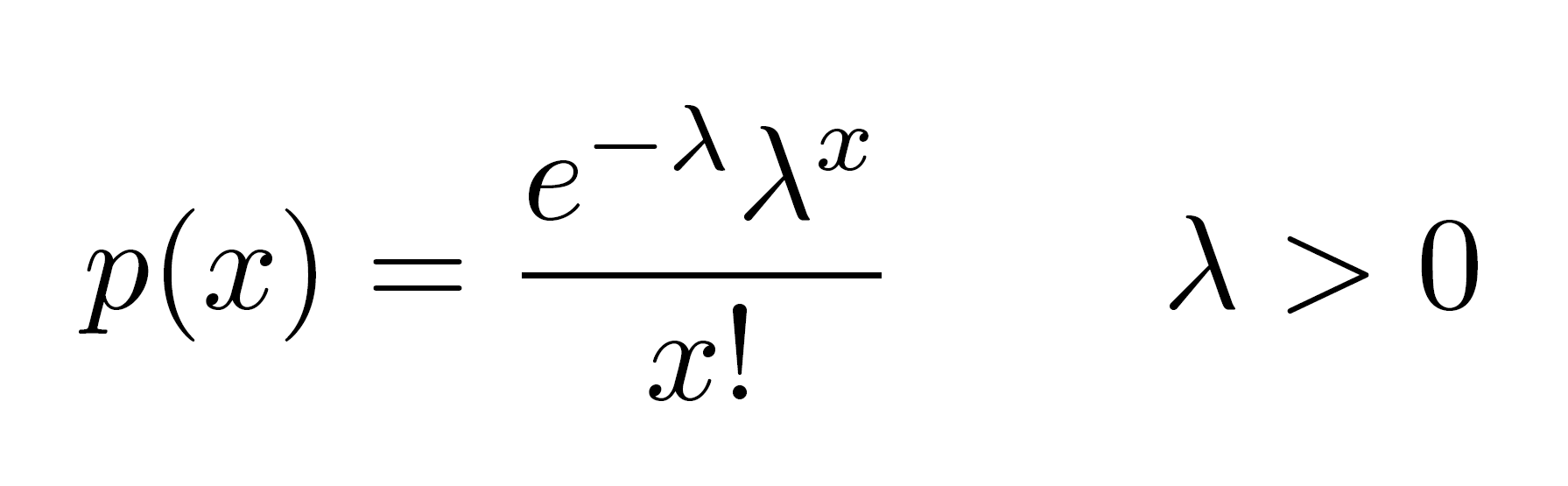
dove λ rappresenta il tasso medio. Possiamo quindi trattare il numero di gol segnati dalla squadra di casa e quella in trasferta come due distribuzioni di Poisson indipendenti. Il grafico qui di seguito mostra la proporzione di gol segnati comparata con le stime fatte attraverso le distribuzioni di Poisson (sulle ordinate, la percentuale delle partite).
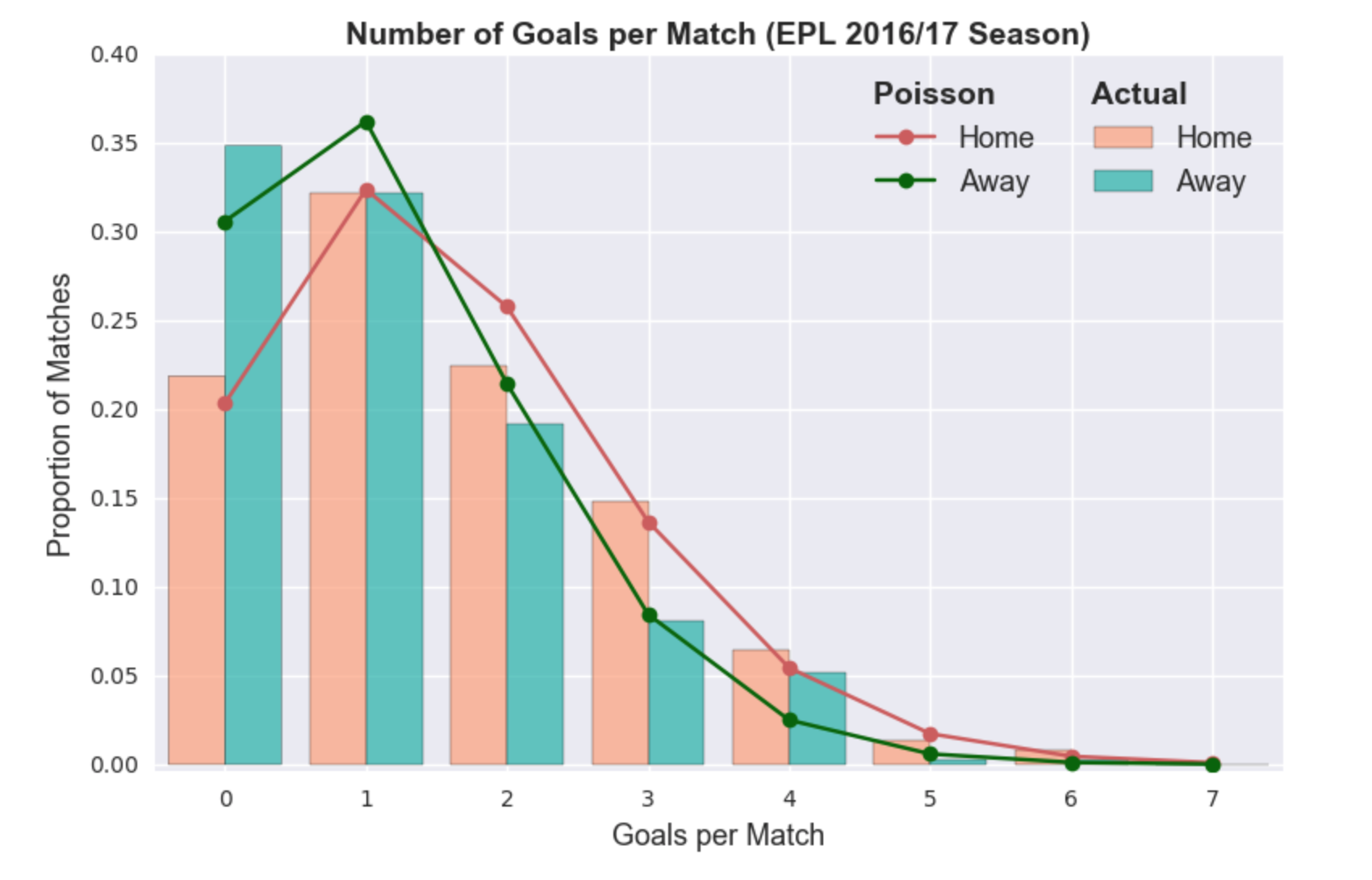
Possiamo allora usare questo modello statistico per stimare la probabilità di un evento specifico: ad esempio, la probabilità che la squadra di casa segni più di due gol risulta essere
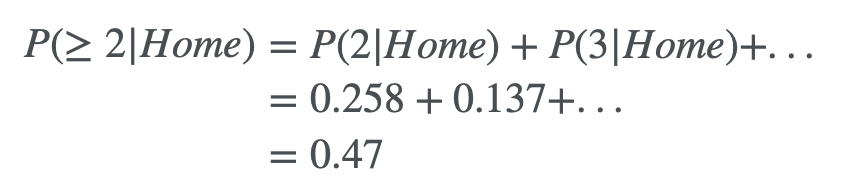
La probabilità che le due squadre pareggino è semplicemente la somma degli eventi in cui le due squadre segnano lo stesso numero di gol:
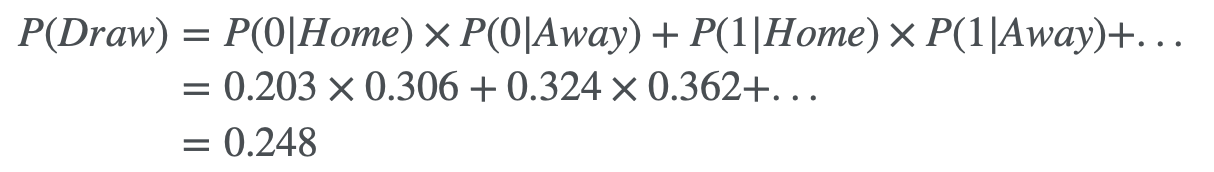
A questo punto spero che possiate capire come è possibile adattare questo approccio: è necessario sapere quanti gol in media segna ciascuna squadra e inserire questo dato nel modello di Poisson. Diamo un’occhiata alla distribuzione di gol segnati da Chelsea e Sunderland, che hanno finito il campionato rispettivamente in prima e ultima posizione.
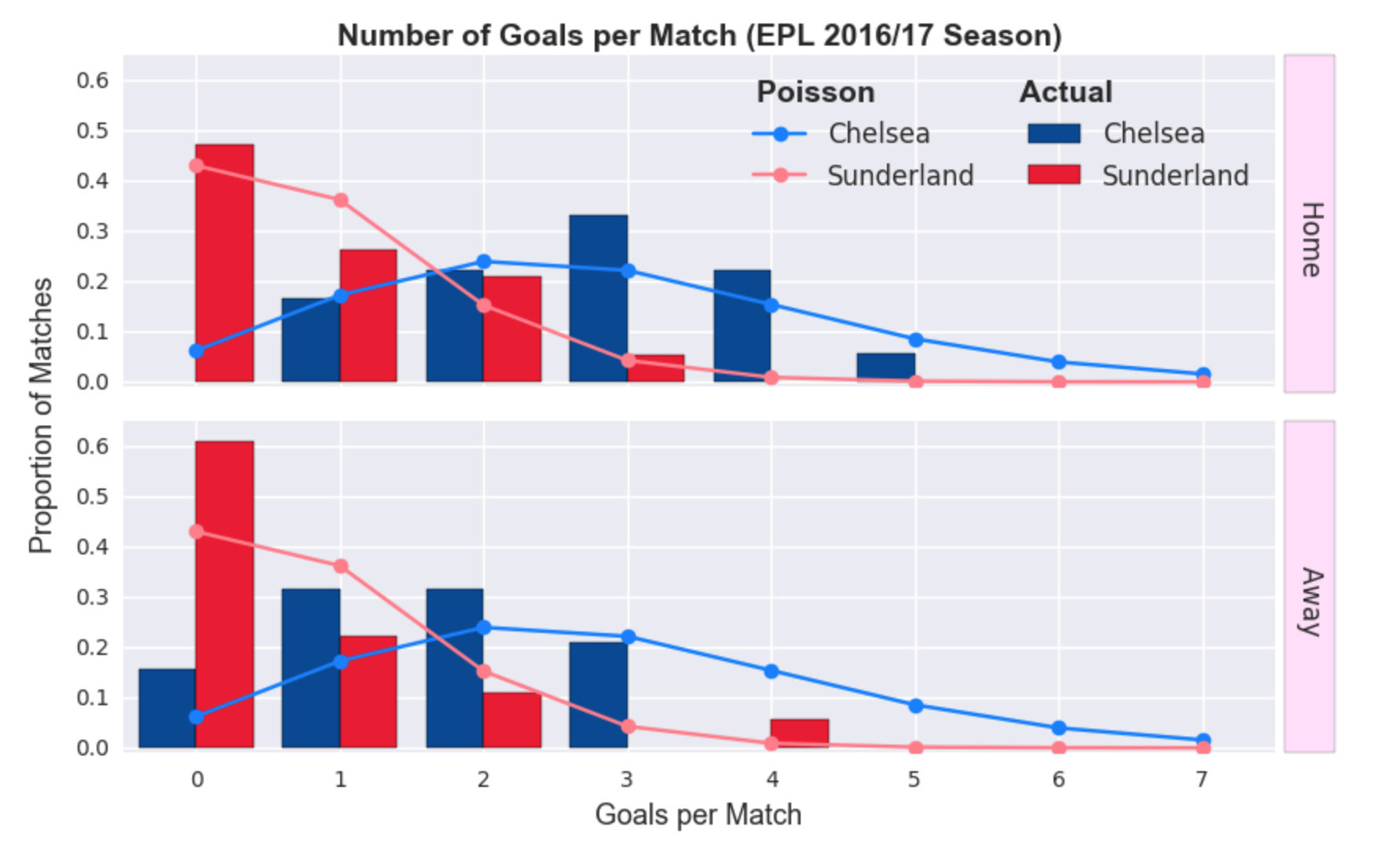
Sembra abbastanza legittimo, ora, assumere che il numero di gol segnati da ogni squadra possa essere approssimato da una distribuzione di Poisson. Iniziamo allora a prevedere i risultati di qualche partita: basta semplicemente passare al modello i nomi delle squadre e questo restituirà il numero medio di gol stimato per ogni squadra; vediamo quindi quanti gol si stima che Chelsea e Sunderland segneranno.
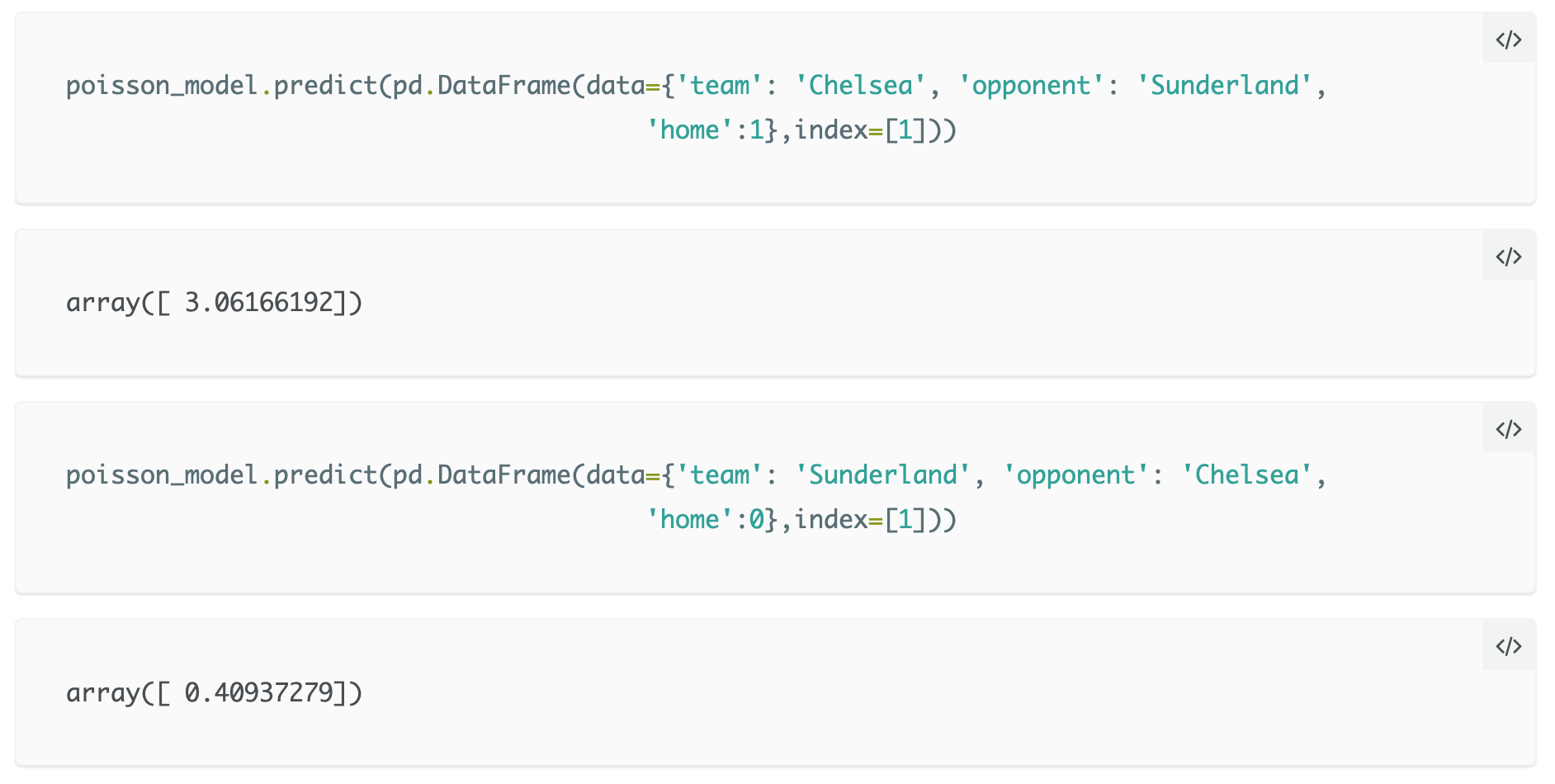
Proprio come prima, abbiamo due distribuzioni di Poisson. Da ciò, possiamo calcolare la probabilità di vari eventi. Per fare ciò viene creata la funzione “simulate_match”.
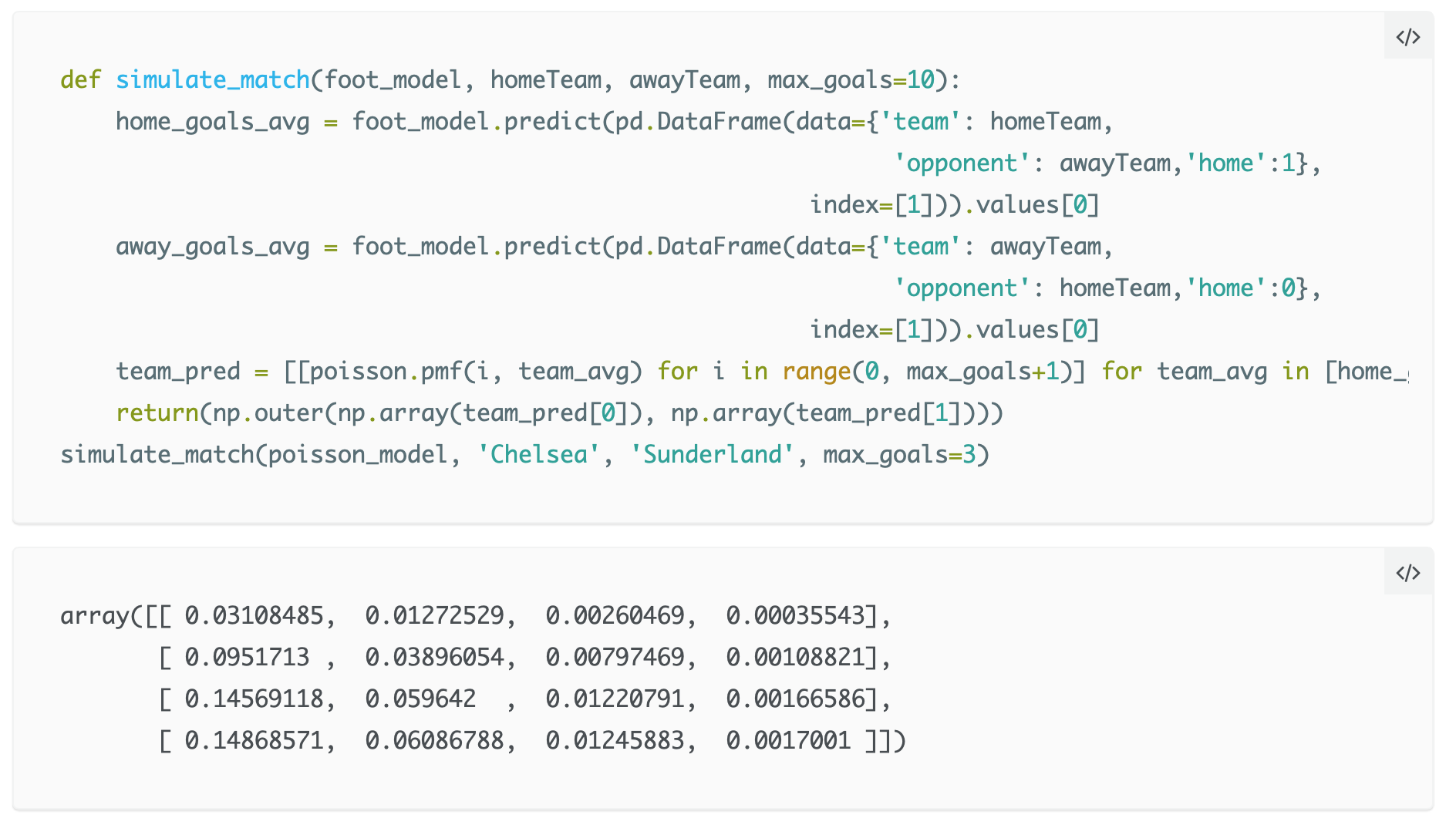
Questa matrice mostra semplicemente le probabilità che Chelsea (righe della matrice) e Sunderland (colonne della matrice) segnino uno specifico numero di gol; per esempio, sulla diagonale, entrambe le squadre segnano lo stesso numero di gol (per esempio P(0-0)=0.031). Si può quindi calcolare la probabilità di un pareggio sommando tutti i termini sulla diagonale; allo stesso modo si può ottenere la probabilità che il Chelsea vinca sommando tutti i termini posti sotto la diagonale, quella che il Sunderland vinca con i termini posti sopra. Per fortuna, è possibile utilizzare delle funzioni di manipolazione delle matrici per eseguire questi calcoli.
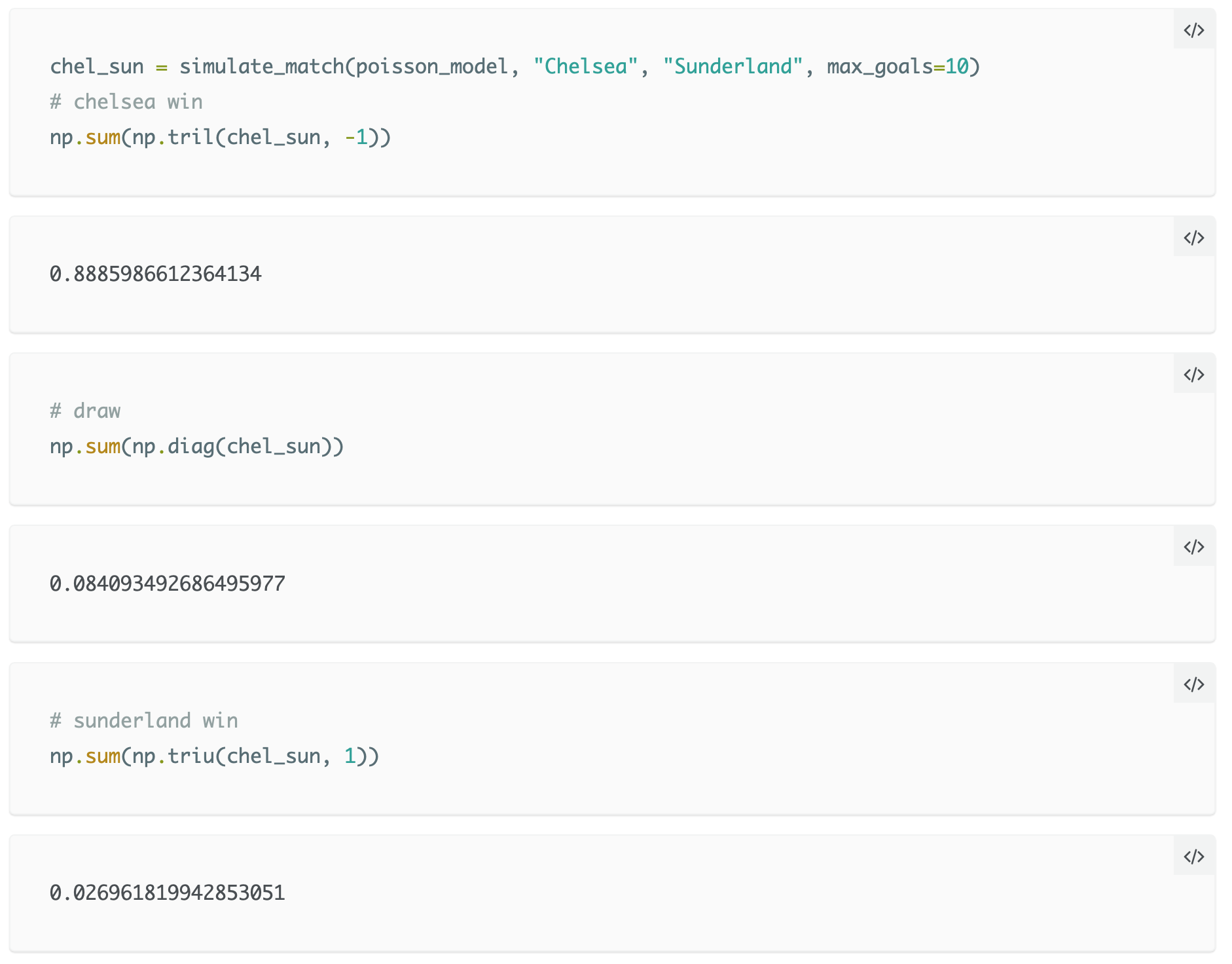
Il fatto affascinante che entra in gioco in questo discorso, dunque, è che ogni partita genera milioni di dati. Se sport come basket, football americano e baseball hanno giù una lunga storia di analisi statistica alle spalle, il calcio è solo l’ultimo arrivato nel mercato. Nel film del 2012 Moneyball, tratto da una storia vera, gli allenatori della squadra di baseball devono affrontare le ristrettezze economiche della società nel budget per costruire la squadra e, per risolvere il problema, utilizzano un sofisticato approccio orientato all’analisi statistico per studiare le statistiche dei giocatori con cui formare la rosa; alla fine è proprio questa squadra, composta da talenti di secondo piano, a vincere ogni partita, dimostrando quindi il successo dell’approccio analitico. In questo decennio è avvenuto il contatto tra data science e calcio, se nel prossimo avremo un nuovo caso moneyball ce lo dirà solo il tempo.
